量子化学計算に関係する用語を調べた覚え書きとして作成したものです。




　

最高被占軌道	電子が入っている軌道のうちエネルギーが最も高い軌道のこと。HOMO（highest occupied molecular orbital)という。 フロンティア軌道 の一つ。
最低空軌道	電子が入っていない軌道のうちエネルギーが最も低い軌道のこと。LUMO(lowest unoccupied molecular orbital)という。 フロンティア軌道 の一つ。
三重結合	六個の電子を共有している結合。結合次数が3ということ。（結合性軌道にある電子数-反結合性軌道にある電子数）÷2＝3
三重項状態	多重度参照
磁気量子数（ｍ）	電子の角運動量の大きさを表す量子数で磁気的な性質と関係する。方位量子数ℓと　ｍ＝0、±1、±2、・・・±ℓ　の関係がある。例えば水素原子の1ｓ状態は方位量子数がゼロだから磁気量子数もゼロとなり磁場の影響を受けない。方位量子数が1の2ｐ状態は磁気量子数が-1、0、1の三種類あり、ゼロの時は磁場の影響を受けずそのエネルギー固有値は2ｓと同等。±1の状態は磁場の影響を受ける。結局主量子数ｎが2の時はエネルギー固有値が三つに分かれる。 　このことは磁場の中で水素原子のスペクトルを観測することにより確かめられる。
下向きスピン	スピン量子数が-1/2の状態を習慣的に下向きスピンという。また、下向きスピンの状態を「β」と表す。
遮蔽効果	有効核電荷を参照
主量子数（ｎ）	シュレーディンガー方程式を水素原子について解くと、電子の持つエネルギーは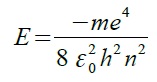             　　　　　 と表される。ここに出てくる ｎ が主量子数で　ｎ＝1の時エネルギーは最低値となり絶対値で13.6eVとなる。これは水素原子のイオン化エネルギーに他ならない。このように主量子数はエネルギー固有値に直接関係しており、主量子数が大きくなるほど水素原子のエネルギーは高くなる。
シュレーディンガー方程式	波動方程式ともいう。次のような二階微分方程式の形をしている。簡単のため粒子がｘ方向に運動している一次元の場合を示します。 　　　　　　　 　 左辺の｛　｝の中をＨ（ハミルトン演算子という）とおきかえて　ＨΨｘ＝EΨｘ　という形になります。Ｈの中身の第一項は粒子の運動エネルギーを、第二項はポテンシャルエネルギーを表します。 　この方程式を解くことにより粒子の持つエネルギー（E）と、各エネルギー値の波動関数を求めることができます。
初期軌道	繰り返し計算によってよりエネルギーの低い分子軌道を決定するＳＣＦ計算において出発点となる分子軌道のこと。Ｆｉｒｅｆｌｙでは拡張ヒュッケル法で初期軌道を求めるＨＵＣＫＥＬと、一電子ハミルトニアン演算子を使って求めるＨＣＯＲＥの二つのオプションがある。
水素結合	窒素、酸素、フッ素など電気陰性道の大きい原子と結合している水素は、相手に電子を引き寄せられて部分的に陽電荷を帯びる。このような水素は電気陰性度の大きい原子の非共有電子対との間に引力を生ずる。この引力によって分子間で形成される結合を水素結合という。 　水素結合の強さは10〜40kJ/molで共有結合の150〜1000kJ/molに比べ弱いものだが、水の場合も非常に多くのＯＨ---Ｏの形の水素結合が起こり劇的な効果をもたらす。それは水の沸点（１００℃）に現れており、この温度は水素結合がない場合に予想される沸点より２００℃も高いと言われている。
スピン量子数（ｓ） スピン磁気量子数（ｍｓ）	電子スピンの状態の違いによって二種類の磁気モーメントを持つと考えられる。このことを表すために、電子が原子核の周りをまわる軌道角運動量の方位量子数（ℓ）と磁気量子数（ｍ）の関係　ｍ＝‐ℓ、‐ℓ+1・・・ℓ-1、ℓ　 の類推から、電子のスピン量子数を1/2、スピン磁気量子数を　-1/2、1/2　と定めた。 　デイラックの相対論的量子力学からこのような角運動量の量子数が反整数の粒子が自動的に出てくるそうだ。
生成熱	化合物1モルが成分元素の単体から生成するときに発生、または消失する熱量のこと。生成熱の値が小さいほどその物質は安定し ているといえる。
静電相互作用	極性分子（分子全体として電気的な偏り＝双極子モーメント）を持つ分子やイオンの間に働く静電力。
相対論効果	周期表四列目以降にある重原子では内殻電子の運動が高速になり、光の速度に近づくにつれ相対論の効果で質量が増加する。その結果ｓ軌道やｐ軌道の電子分布が収縮し核電荷をより遮蔽するためｄ軌道やｆ軌道は拡張する。 　周期表六列目のＰｔの内殻電子は光速の57％で運動していてそのエネルギーは22％も増加する。この効果は原子量が多きくなるほど顕著になり、物性に影響する。